- 2011.09.19. 22:23
Múlt hét kedden indult 3 részes interjú sorozatunk középső részét olvashatjátok Erdély Dániel feltaláló és antropológus életéről.
(Szerző: hna)

A sok harc, kutatás és utána járás mellett mégis miből tudtál megélni az utóbbi időben?
1981-től, míg apám élt és még utána is néhány évig kreatív falburkolatokkal kerestük a pénzünket, de én közben egyfolytában rajzoltam, céges arculatokat terveztem, szakmám szerint. Nagyon szerettem, szeretem a logókat, meg a kiállítások designját, a kiállítási grafikákat. Az Artex megbízásából Ortutay Tamással és Megyik Jánossal a Lego-nak terveztünk ládákat. Ezek olyan jól sikerültek, hogy nívódíjat vagy valami olyasmit kaptunk érte a Lektorátusban. Később ez lett az alapja a dániai ösztöndíjamnak, ahol a Lego tervezőjével személyesen is megismerkedhettem. Volt bennem mindig egy konstruktív hajlam, építészeti érdeklődés is, nagyon érdekelnek a szerkezetek, csomópontok, meg ilyesmik. A geometria és a logika pedig mindig különösen érdekelt. Még gimnazista koromban részt vettünk a bátyámmal, Gyurival az egyik Gondolkodás iskolája pályázaton. Az arról szólt, hogy egy éven keresztül meg kell fejteni nagyon nehéz problémákat. Megoldottuk az összeset. 16-ikak lettünk az országban, úgyhogy azért az nem volt semmi. A PhD-írás adott egy kis teret és időt arra is, hogy a Spidron témába még jobban belemerüljek. E közben édesanyám lakásának kiadásból és kisebb munkákból tudtam fedezni nagyjából az élet költségeit.
Sokszor említed, szüleidet, rokonaidat, gyermekeidet? Mennyire fontos az életedben a család?
Nagyon fontos a család. Egyrészt ezt a példát láttam magam előtt, másrészt apám utolsó éveiben rengeteget dolgozott, festett és ennek köszönhetően egy elég nagy hagyatékot hagyott ránk. Mikor meghalt, a bátyámmal hirtelen lettünk a „család öregjei”, mert szinte egyszerre hunyt el a nagybátyám, a nagyapám és az apám is. Akkor nagyon nagy teherként, de egyszersmind édes teherként zúdult ránk ez a hagyaték. Anyám segített sokáig, de ő is beteg lett, 12 évig betegen éldegélt. Egy kórházi kezelés kapcsán megkapta a hírhedt hepatitis C vírust, és még kártérítés se járt neki, mert még akkor nem fedezték fel ezt a vírust. Úgyhogy nagyon-nagyon rossz lelki és egészségi körülmények között éltünk, de én nem vesztettem el a lelkesedésemet. Ahogy tudtam, vigyáztam is magamra és talán szerencsém is volt. Nagyjából rám volt bízva a családban a hagyaték átmentése nyugodalmasabb időkre, ahogyan most a fiamra, Simonra, aki apám hét unokája közül átvállalta ennek a munkának a nagy részét. Úgy tűnik, egyelőre szívesen és nagy ügyszeretettel, hozzáértéssel csinálja.

Térjünk vissza a Spidronra egy picit! Hol debütált a Spidron, ha egyáltalán volt ilyen?
A Spidron téma sokáig lappangott, de nagy lökést adott, amikor kiutaztunk a családdal az Egyesült Államokba 1990-ben. Ott volt négy hónapom, amikor sikerült egy zárt térbeli Spidron-formát létrehozni. Amikor visszajöttem, találkoztam egy román optikai kristályfizikusnővel, Cristiana Grigorescuval, aki azt mondta, hogy ez fantasztikus, mutassam be Jeruzsálemben a következő kristálynövesztési világkonferencián. Mondtam, hogy „Ho-hó, hogyne! Nem vagyok én olyan jó angolból, tudósok közé nem szoktam menni előadni!”, de olyan ügyesen, kedvesen írogatott, képeslapozgatott, hogy végül mégis rászántam magam, és – lássatok csudát! – sikerült.
Tehát 1998-ban Jeruzsálemben, a 12. Kristálynövesztési Világkonferencián debütált a Spidron nemzetközi nyilvánosság előtt. Egy eléggé megosztó előadást tartottam, mivel voltak, akik ujjongással, de akadtak, akik cinizmussal fogadták geometriai fejtegetéseimet. Viszont azért annyi hatása volt a megmozdulásomnak, hogy hazatérvén meghívtak az MTA szegedi épületébe, aztán Budapesten a Rényi Alfréd Matematikai Intézetben is előadást tarthattam, továbbá megjelentem tudományos publikációkban is. Aki kint meg merte magát próbálni – ami a kilencvenes években elég nagy dolog volt –, annak itthon már nagyobbak voltak az esélyei.

Mi volt a legérdekesebb dolog a Spidronnal kapcsolatban?
Van egy máig működő portál (SuliNet), amelynek a szerkesztője, Taracsay Tamás. Ő bemutatott engem Szegeden egy matematikusnak, Szilassi Lajosnak, aki teljes energiájával azon volt, hogy megcáfolja az általam megvalósított Spidron-mozgást. Heteket, hónapokat szánt rá, és végül kijött neki, hogy mégis nekem van igazam, létezik ez a mozgás. Annyira megdöbbent, hogy azt mondta , hogy "Ez egy olyan jó téma, hogy írjunk egy dupla cikket róla!" Az övé itt olvasható.
Az előadások a konferenciakötetben jelentek meg Pécsett, aztán a Karlsruhe-ban is. Bemutattuk egy közös előadás formájában a Hajtásválogatás elnevezésű nemzetközi konferencián a pécsi Pollack Mihály Műszaki Főiskolán is. Tulajdonképpen akkor lett meg a Spidron első algoritmusa egy nagyon hosszú matematikai képlet formájában. Maga Szilassi Lajos mondta, hogy amikor beírta a paramétereket, akkor a MAPLE nevű matematikai program kiadott egy tizenhat-soros képletet. Erről azt tudta, hogy, ha a Spidron-mozgás valós, akkor annak nullával kell egyenlőnek lennie. Valamennyire tudta egyszerűsíteni, és hát nyilván "milliószor" átnézte, hogy ne legyen benne hiba, és kijött neki, hogy az eredmény valóban nulla. Attól kezdve a Spidron matematikai entitássá vált, és akkor végre számítógépre lehetett vinni. Elkezdtek özönleni a Spidron lények százasával. Véleményem szerint ez az eredmény visszahatott az egész geometriai gondolkodásra, de először csak óvatosan mertem ezt kijelenteni.

Mikor 29 év után igazolták az elméletedet, mit éreztél?
Természetesen nagyon örültem, de a legtöbb időm mégis arra ment, hogy nem hittem el, hogy ilyen korábban még nem volt. Kerestem valahol a szakirodalomban, meg mindenféle irodalomban. A japánok elég közel kerültek hozzá a 90-es években, de nem volt még nekik sem meg a hasonló modell. Azóta már egy csomó minden van persze. Ellopkodni nem nagyon lehet, mert ez már – mintegy harminc-negyven külföldi és hazai előadás, kiállítás után – hozzám kötődik.

Miért pont Spidronnak nevezted el a találmányod?
A Spider pókot jelent angolul és az alakzataim pókhálószerűek. Nagyapám pedig Spitzer-ről magyarosította a nevét a 20. század elején Erdély-re.
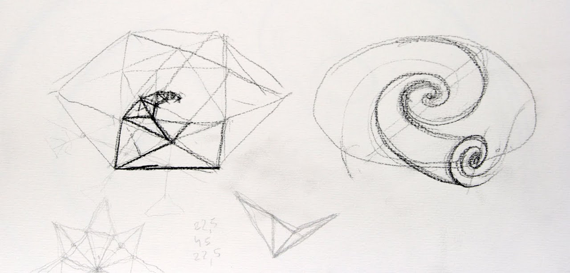
Volt segítséged a Spidron kutatás során?
Hosszú ideig alig, de meg kell említenem Kiss Gergő és Kőszegi Péter nevét, akik a kilencvenes évek végén fontos ábrákkal és animációkkal járultak hozzá a deformációk bemutatásához. A szoftverek is lassan fejlődtek odáig, hogy alkalmassá váljanak a bonyolult mozgások ábrázolására. Egy idő után az interneten és külföldi útjaim során találkoztam olyan érdeklődőkkel, akik később bekapcsolódtak a fejlesztésbe. A Rhino nevű modellező program megismerése hozott össze Rinus Roelofs-szal, akivel évekig dolgoztunk később együtt. Hamarosan egy nemzetközi team állt össze körülöttem. Meg kell említeni Marc Pelletier, Amina Buhler-Allen és Craig S. Kaplan nevét. Együtt dolgoztunk a Spidronnal kapcsolatban a geometria száz területén. Példaként mondom, hogy vannak ún. minimál felületekkel burkolt testek. A minimál felület tömören és konyha-nyelven olyan felületet jelent, amelyet szappanbuborék, szappanhártya darabokból, tehát a legkisebb feszültségű felületekből (térbeli rombusz felület = nyeregfelület) lehet összeállítani. 2009-ben Walt van Balleggooijennel és Paul Gailiunasszal 42 olyan Spidron-felületekkel határolt testet alkottunk és adtam be mintaoltalomként a Magyar Szabadalmi Hivatalba, amely önmagában, tehát saját másolataival kitölti hézagmentesen a teret, akár a tégla vagy a kocka. Ez azt jelenti, hogy nagyon jól számítható, tervezhető, változtatható elemekről van szó. Előadtuk az elképzeléseinket Kanadában is. Ekkor már a Spidron teamnek holland, angol, litván származású, angol, amerikai, kanadai és magyar tagjai is voltak. A magyarok közül a már említett Szilassi Lajos és Molnár Emil mellett Erdős Janó alkotott maradandót a legutóbbi korszakig.

Épp csak igazolták a Spidron téziseidet és úgy tudom máris továbbfejlesztetted azt? Hogy fogadta a SpHidront a tudóstársadalom és a segítőid?
Gyakorlatilag összevesztünk a teammel. Ők még javában dolgoztak ezeken a térkitöltőkön, én meg elkezdtem az íves felületekkel való foglalkozást. Míg a Spidronnak az a lényege, hogy minden egyes darabja, része síkháromszög, ezért nem volt nehéz megsejteni, hogy kell lennie egy íves változatának is. Ezt nevzetm el SpHidronnak. Mivel az íves felület szabadabb, mint a merev, ezért valószínű, hogy arra is rá lehet találni, csak még bonyolultabb a leírása. Emiatt elkezdtem tanulni a görbült felületek geometriáját. Olyan topológiával is kellett foglalkoznom, amely nem nyúlós „gumifelületekkel”, hanem mérettartó alakváltozásokkal foglalkozik. Meglepetésemre a barátaim nagyon-nagyon durván, határozottan és agresszíven ellenem fordultak, mondván, hogy, amit állítok az lehetetlenség. Később azonban kiderült, hogy a tulajdonképpen jó szándékú támadások oka abban állt, hogy a SpHidronokban nem triviálisan látható, rejtett szingularitások vannak. Ezek mégis lehetővé tehetik a kérdéses deformációkat, amennyiben azon spirálkarok körül fordul el a sík, amely spirálkarokat ez a fölpödrődő sík közben el is takar. Talán ezért nem vették észre, hogy van ott valami plusz lehetőség, pedig Molnár Emil jelezte, hogy „Lehet igazad, ha van a felületen szingularitás!”. Beadtam egy ezzel kapcsolatos cikket a Bridges nemzetközi tudományos művészeti konferenciára, amelyen idén a hetedik alkalommal vettem részt. A matematika és a geometria mellett téma a zene, színház és az építészet is. A konferenciakötet szerkesztője, a Nobel-díjas csapattag, fizikus-matematikus Carlo Sequin a Berkeley Egyetemről írt vissza, hogy csupán apróbb módosításokkal és pár nyelvi hibával kell megbirkózom és akkor elfogadják a cikkemet. Nagyon örültem és néhány hete elő is adtam Portugáliában az új elméletet. Sajnos ezt egyelőre nem tudták informatikailag követni, tehát nincs kollégám, aki pillanatnyilag ezt egzakt módon számítógépre vihette volna a konferenciára. Elkezdtem tehát szabad kézzel és ecsettel rajzolni, festeni és csináltam körülbelül 100 vázlatot, amelyekkel ezt a deformációt illusztrálni tudtam. Ezeken próbáltam bemutatni Coimbrában, hogy mire gondolok. Nagyon új dolog ez. Nehéz elmagyarázni, de úgy vélem, hogy komoly alapja van annak, amit állítok. Már létre is hoztunk az említettekhez hasonló íves csavart felületeket. Tarajok és sima spirálok mentén fölpöndörödő síkokkal lehet parkettázni a síkot, és lehet alkotni térbeli alakzatokat is. Ilyen modellek ténylegesen létrejöttek a közelmúltban Torolf Sauerman és Paul Nylander segítségével. Az a szép ebben, hogy ha kivágok ebből a felületből négy- vagy hatszögeket, azok ugyanúgy összeilleszthetők és ugyanúgy folyamatos felületet adnak, mint hogyha sík hatszögeket raknék össze. Reméljük, nem kell újabb 29 év, hogy ezt a sejtésemet is igazolják…